• alapok
• asymmetric encryption
• digital signature
• dokumentáció
• hash
• key derivation
• MAC
• provider
• quantum computer
• secure random
• symmetric encryption

• Kriptográfiai alapműveletek:
  • Titkosítás (encryption)
  • Visszafejtés (decryption)
  • Hash készítés
  • Kulcsok kezelése (secret key, private key, public key)
• A titkosítás/visszafejtés 2 módja:
  • symmetric encryption
  • asymmetric encryption
• Érzékeny adatok továbbításához biztosítani kell hogy az illetéktelen személyek:
  • Ne tudják értelmezni.
    Megoldás: az adat titkosítása.
  • Ne tudják módosítani.
    Ezt nehéz biztosítani, de megoldható, hogy ha az adat módosul, akkor a címzett észrevegye.
    Megoldás: az adatot titkosítani kell, az adatból képzett hash-t is titkosítani kell, majd mindkettőt el kell küldeni a címzettnek.
    A címzett mindkét adatot visszafejti, és ellenőrzi, hogy a hash az adatnak megfelelő-e.
• A titkosítást, és visszafejtést a Cipher osztály végzi, de az algoritmusokat a Provider-ek biztosítják.
• A java képes a kulcsokat kulcs tárolóban (keystore) tartani.
• A tanúsítvány (certificate) egy olyan dokumentum, mely bizonyítja a publikus kulcs hitelességét.
  Tehát egy publikus kulcshoz kapcsol egy személyt vagy egy domain nevet.

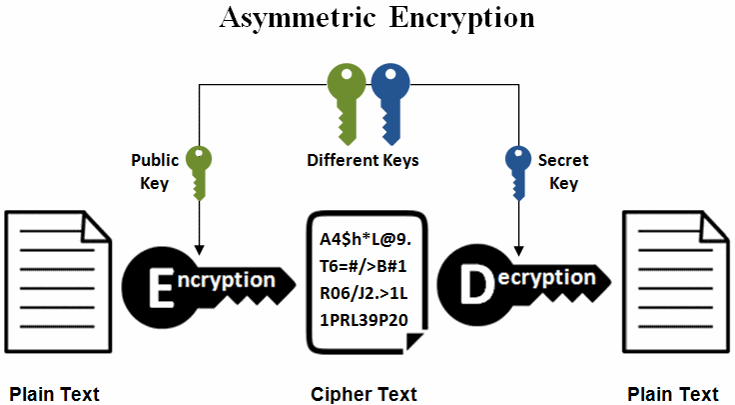
• Aszimmetrikus titkosítás
  Különböző kulcs kell a titkosításhoz és a visszafejtéshez: private key és public key.
  A private key, és a hozzátartozó public key egy kulcs pár-t alkotnak.
  A privát kulcsot rejtve kell tartani, a publikus kulcs pedig bárkivel megosztható.
  
• Lassabb mint a szimmetrikus titkosítás, és csak kisebb adatot lehet vele titkosítani.
• A privát kulccsal történik a titkosítás, és a publikus kulccsal a visszafejtés, vagy a publikus kulccsal történik a titkosítás, és a privát kulccsal a visszafejtés.
• Modern algoritmusok: RSA, ECC (Elliptic Curve Cryptography), Diffie-Hellman, ECDH, ECDSA and EdDSA.
  
• Még a modern algoritmusokra is jellemző a quantum-breakable, tehát legalábbis elméletben egy igen nagy teljesítményű quantum számítógéppel meghatározható a publikus kulcsból a privát kulcs.
• RSA
  • Az RSA volt az első komoly algoritmus, mely a mai napig is használatban van.
  • Azért sem lehet vele nagy adatot titkosítani, mert az adatból egy egész számot kell képezni, és ezt az egész számot kell titkosítani.
  • A titkosítás 1000-szer lassabb mint a szimmetrikus AES algoritmusnál.
  • Kulcs hossz: 1024, 2048, 3072, 4096, 8129, 16384 bit, vagy több.
    A 3072 bit, vagy nagyobb kulcshossz biztonságos.
    A nagyobb kulcshossz jobb biztonságot, de hosszú előállítási időt jelent.
  • A publikus kulcs nem állítható elő a privát kulcsból.
• ECC
  • A privát kulcs tipikusan 256 bites, ami egy véletlenszám, így nagyon gyorsan előállítható.
  • Modernebb mint az RSA, mert magasabb biztonságú, és rövidebb kulcsokat használ.
  • A publikus kulcs a privát kulcsból előállítható.
  • Egy 256 bites ECC kulcs hasonló erősségű mint egy 3072 bites RSA kulcs.
  • Az RSA-val szembeni előnyéből fakadóan a blokklánc hálózatok, mint például a Bitcoin és az Ethereum az ECC algoritmust használja a tranzakciók biztosításához.
• Hybrid encryption
  Ezt a módszert az aszimmetrikus titkosítás hátrányai miatt alkalmazzák.
  Kombinálja a szimmetrikus és aszimmetrikus titkosítást:
  A titkosításhoz generálnak egy szimmetrikus kulcsot: SK
  Az adatot titkosítják az SK-val, majd az SK-t titkosítják a privát/publikus kulccsal.
  A fogadó oldalon a privát/publikus kulccsal visszafejtik az SK-t, majd az SK-val visszafejtik az adatot.
• Java programban az aszimmetrikus titkosítást és visszafejtést a Cipher osztály végzi.
  A programkód hasonló mint a szimmetrikus titkosításnál, csak itt aszimmetrikus algoritmust kell használni,
  és a kulcspár más-más tagjával történik a titkosítás és a visszafejtés.
• Kulcs pár generátor használata:

• Digitális aláírás
  Az aláírandó dokumentumról (bájtsorozat) hash-t kell készíteni, és a hash-t titkosítani a privát kulccsal.
  Az így keletkező fájlt nevezzük digitális aláírásnak. A műveletet a Signature osztály végzi.
• A Signature osztály alkalmas arra is, hogy a már elkészült digitális aláírást ellenőrizze. Ellenőrizni a publikus kulccsal lehet.
• Így tehát egy dokumentum utazhat a digitális aláírásával együtt 2 fájlban, lehet hogy a dokumentum nem is titkosított, de a digitális aláírás bizonyítja hogy valós.

• Jenkov: Java Cryptography
• Nakov: Practical Cryptography for Developers

• Hash
  Egy tetszőleges dokumentum (bájtsorozat) adataiból egy fix hosszúságú adat képzése.
  Például, a dokumentum bájt értékeit pozitív számként értelmezve összeadjuk, majd az összeget maradékosan elosztjuk 256-tal. A maradék (0-255) lesz a hash. Ez az algoritmus bármely dokumentum esetén 1 bájtos hash-t képez. Nevezzük el "h1"-nek.
  A "h1" egy működőképes algoritmus, de nem felel meg a szigorú kriptográfiának, ugyanis egyéb feltételeket is teljesíteni kell:
  • Deterministic (meghatározó):
    Egy dokumentum esetében a hash algoritmusnak mindig ugyanazt a hash-t kell adnia.
  • Collision-resistant (ütközés mentes):
    Nem található 2 olyan dokumentum, mely ugyanazt a hash-t adja.
    A mai modern kriptográfiai hash algoritmusoknál nincs egyetlen ismert ütközés sem.
  • Irreversible (visszafordíthatatlan):
    A hash-hez nem található meg az a dokumentum melyből készült. Pontosabban nincs olyan algoritmus mellyel előállítható lenne a dokumentum belátható időn belül. Nem belátható időn belül persze létezik, hiszen csak a világ összes dokumentumát kellene végigpróbálni.
  A "h1" nem teljesít 2 feltételt, mert:
  Példa ütközésre: h1('abc') = h1('cba') = h1('bac')
  Példa dokumentum előállításra: az egybájtos dokumentum pont egyezik a hash-értékével.
• Az ideális hash algoritmusoknál ezeknek is teljesülnie kell:
  • Quick (gyors)
  • Hard to analyze:
    Egy kisebb (pl. 1 bájt) módosítás a dokumentumon teljesen más hash értéket ad eredményül.
• Hash felhasználása:
  • Integrity (sértetlenség): egy dokumentum mellett a hash értéke is nyilvános, így ellenőrizni lehet vele, hogy a dokumentum nem változott. Ha mégis, akkor más hash tartozna hozzá.
  • Storing password: egy adatbázisban nem plain-text-ként tároljuk a jelszavakat, mert így könnyen kiolvasható, hanem a password-ből hast-t képzünk, akár többször is, és azt tároljuk.
    "Password salt": a jelszót kiegészítjük egy véletlen szöveggel (salt), és abból képezzük a hash-t. Így az adatbázisban letárolható a véletlen szöveg, és a hash. A kapott hash nem lesz megtalálható hash-táblákban (hash-table resistant).
  • Generate unique ID: egyedi azonosító előállítása a dokumentumból. Ellenőrizhető vele, hogy van-e már ilyen dokumentumunk. Dokumentum dupla tárolás elleni védelem.
  • Véletlenszám generálás: igazi véletlen eseményekből (random seed), előállítható egy hash, de akár tetszőleges sok ha a random seed-hez hozzáírunk 1-et, hajd abból hash-t képezünk. Hozzáírunk 2-t, majd abból hash-t képezünk, ...
  • Proof of work (a munka bizonyítéka): Bányászok által használt módszerek elnevezése, amikor akár több billiónyi hash műveletet kell elvégezni. Példa: Egy adott X-hez találjuk meg azt a P-t, ahol a hash(x + p) értéke 10 darab 0-ás bittel kezdődik.
• Hash többféle algoritmussal készíthető.
  Nem biztonságos, ne használjuk: MD5, SHA1. Több ütközés (collision) is előfordul a használatukkor!
  Biztonságos, a mai kornak megfelelő modern hash algoritmusok: az SHA2 és SHA3 család tagjai, például: SHA-256, SHA-384, SHA-512
• Hash-t a MessageDigest osztállyal lehet készíteni, például: Ha az adat túl nagy, akkor az adat részleteivel is el lehet készíteni a hash-t a messageDigest.update() metódus többszöri meghívásával.

• Gyakran megtörténik, hogy viszonylag könnyen megjegyezhető jelszóból állítjuk elő a titkos kulcsot. Ezt könnyen meg lehet tenni egy sima hash függvénnyel, azonban ez nem biztonságos. Ugyanis az így keletkező hash egy jelszó feltörő hash adatbázisban (hash-table, rainbow-table) szerepelhet, és onnan megvan a jelszó is.
  Az is megoldás, hogy nem csak egy sima hash-t hajtunk végre a jelszón, hanem a hash-t újra hash-eljük (hash-lánc), de közben módosítunk is rajta. A jelszó mellé beiktathatunk egy salt-ot, vagyis egy másik bájtsorozatot, és ez is része lehet a hash-nek.
  Ezenkívül léteznek komolyabb algoritmusok is erre a problémára: Scrypt, Bcrypt, Argon2

• MAC = Message Authentication Code
• MAC elkészítése: az adatból hash készítése, majd a hash titkosítása a secret key segítségével.
  Tehát a titkosítás mindig szimmetrikus kulccsal történik.
• Akkor hasznos ha 2 ember üzenetet akar küldeni egymásnak (titkosítva vagy sem), de biztosak akarnak lenni, hogy az üzenetet nem módosították útközben, vagyis sértetlen. Ebben az esetben az ábra szerint kell eljárniuk:
  
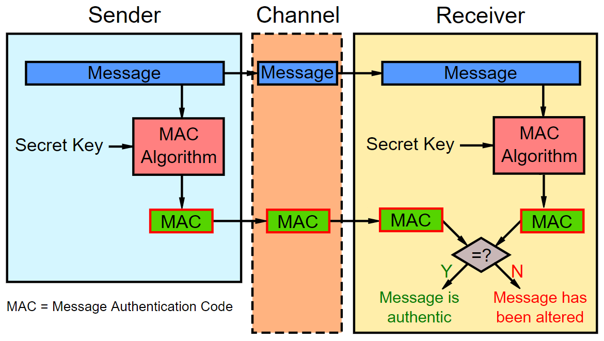
  Tehát a MAC-et senki sem fejti vissza, hanem az adatból a küldő személy elkészíti, a fogadó személy is elkészíti, és a fogadó feladata ellenőrizni, hogy a kapott MAC, és a maga által készített MAC azonos-e. Ha igen, akkor az üzenet sértetlen.
• A MAC készítése többféle algoritmussal készülhet, tipikusan ilyen a HMAC algoritmus.
• MAC készítés példa: Ha az adat túl nagy, akkor az adat részleteivel is el lehet készíteni a MAC-kódot a mac.update() metódus többszöri meghívásával.

• A Java beépített provider-einek, és az általuk támogatott algoritmusoknak a kiiratása: Az algoritmus listát nem pontosan kell értelmezni, mivel ilyen nincs a listában, mégis működik:
• A beépített provider-ek halmazából lehet törölni, és/vagy új provider-t hozzáadni:

• A quantum számítógép nem egy nagyon gyors számítógép, hanem egy olyan számítógép mely speciális problémák megoldására lett kifejlesztve, például a kriptográfia.

• Pseudo random
  Ál véletlen.
  Ilyet állít elő a PRNG (Pseudo Random Number Generator).
  Van egy belső kezdeti állapota, (initial entropy, vagyis seed), és ebből generálja folyamatosan a számokat, és minden szám előállítása után egy új állapotra áll be.
  
  
• Seed (initial entropy)
  Ennek valóban kiszámíthatatlan véletlennek kell lennie, különben ennek ismeretében az összes generált véletlenszám ismert lenne. Olyan eseményekből áll össze, mint egérmozgás, billentyű leütések, mikrofon, ... Akár operációs szinten is előállhat ilyen, amit használhatunk, linux esetén: /dev/random, /dev/urandom
• Secure random
  Kiszámíthatatlan véletlen (unpredictable random).
  Ilyet állít elő a CSPRNG (Cryptography Secure Pseudo Random Number Generator).
  Az initial entropy (seed), még mással is kombinálva van, így biztosítva azt, hogy valóban kiszámíthatatlan legyen.
  Mindig ezt a módszert használjuk a PRNG helyett: SecureRandom java osztály.
  Ne használjuk a Math.random() metódust, mert az nem biztonságos.
• True random
  Ilyet állít elő a TRNG (True Random Number Generator).
  Ezek speciális eszközök melyek a fizikai környezetet figyelik, és ebből állítják elő a seed-et.
  Csak nagyon kritikus biztonsági rendszerek esetén használják, például bank és pénzügyi alkalmazások, certificate authorities (CA).

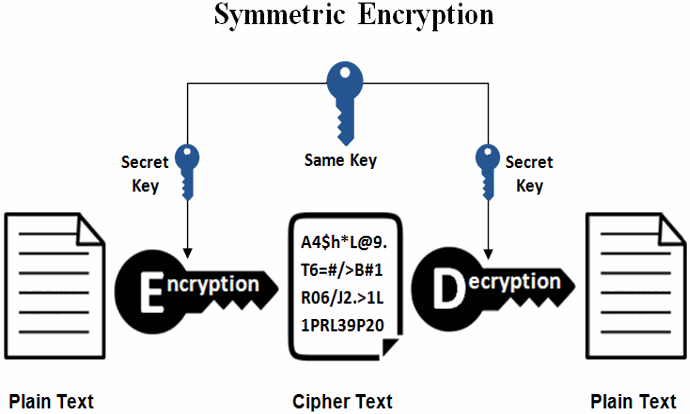
• Szimmetrikus titkosítás
  Ugyanaz a titkos kulcs (secret key) szükséges a titkosításhoz és a visszafejtéshez.
  
• Modern, ajánlott algoritmusok: AES (Rijndael), ChaCha20, Twofish, IDEA, Serpent, Camelia, ...
• Nem biztonságos, nem ajánlott algoritmusok: DES, 3DES, RC2, RC4, Blowfish, GOST, ...
  Ezek általában csak 56 vagy 64 bites kulccsal dolgoznak.
• Ha a kulcs hossza elég nagy akkor quantum-resistant, vagyis quantum-számítógéppel sem lehet feltörni.
• Sokkal gyorsabb mint az aszimmetrikus titkosítás, és tetszőleges nagy adattal el lehet végezni a titkosítást (ellentétben az aszimmetrikus titkosítással).
  A titkosítás nem egyszerre történik az egész adattal, hanem az adat kisebb blokkokra van felosztva, és egyszerre csak egy blokk titkosítása történik meg.
  Egy algoritmuson belül beállítható, hogy milyen blokk-módban dolgozzon.
  Biztonságos, ajánlott blokk-módok: CTR, GCM, CBC
  Nem ajánlott, nem biztonságos blokk-mód: ECB (Electronic Codebook)
• AES algoritmus
  • Kulcs hossz: 128, 160, 192, 224, vagy 256 bit.
  • Blokk méret: mindig 128 bit.
  • Blokk-mód: általában CTR vagy GCM.
  • Ami nagyon biztonságos, és a legjobban ajánlott: AES-256-GCM, vagyis 256 bites kulcs, és GCM blokk-mód.
• AES-t használ a TLS, és SSL protokoll is a https-kommunikációban.
• A titkosítást és visszafejtést a java Cipher osztálya végzi.
• Példa titkos kulcs előállítására.
  Kulcs generátort használunk, melynek alapja egy véletlenszám generátor:
• Példa AES-256-GCM titkosításra, és visszafejtésre.
  A titkos kulcs többféleképpen előállhat, a példában csak egy egyszerű megoldás van rá.
  A titkosítás GCM blokk-módú, ezért meg kell adni a blokk-hosszt, ami AES esetén mindig 128 bit, és egy Initialization Vector-t (IV), amely mindig csak egyszer használatos secure random legyen. Az IV-t tudni kell a visszafejtésnél, mivel ugyanezt kell használni. Ebben a példában nem látható, de a gyakorlatban az IV-t hozzáfűzik a titkosított bájtsorozathoz (elejéhez vagy végéhez). Mivel fix 16 bájt hosszúságú, a visszafejtő könnyen hozzáfér, de ettől még nem törhető fel az adat, tehát a módszer biztonságos.
• Ha az adat túl nagy, akkor az adat részleteivel is el lehet készíteni a titkosítást/visszafejtést a cipher.update() metódus többszöri meghívásával.